오늘은 중등과정 도형에서 많이 나오는 히포크라테스의 초승달에 관하여 알아보도록 하겠습니다.

히포크라테스의 초승달
히포크라테스는 기원전 5세기경에 그리스의 키오스 섬에서 태어났습니다. 그는 상인이었다가 해적들에게 재산을 빼앗긴 후 아테네로 이주하여 수학과 철학을 연구하게 되었습니다. 당시 아테네는 지식의 중심지로, 많은 학자들과 철학자들이 활동하던 곳이었습니다. 히포크라테스는 이곳에서 피타고라스 학파와 교류하며 자신의 수학적 재능을 키워나갔습니다.
그리스 시대에는 유명한 작도의 3대 문제가 있었습니다. 3대 문제란 눈금 없는 자와 컴퍼스만을 가지고 이들을 유한 번만 사용하여, 첫 번째 정육면체의 부피를 두 배로 늘리는 문제, 두 번째 임의의 크기의 각을 삼등분하는 문제, 세 번째 원의 넓이와 같은 정사각형을 그리는 문제입니다.
그 시대에는 도형의 작도가 건축물을 설계하고, 토지를 측량하고, 도시 계획을 세우는 데 꼭 필요한 기술이었습니다. 따라서 도형을 작도하는 방법을 꽤나 공들여 연구하였습니다. 현대와 같이 정밀한 기구가 없었던 고대에는, 모든 도형 문제는 간단한 방법으로 해결해야 했습니다. 그래서 눈금 없는 자와 컴퍼스만으로 문제를 해결하려고 하였지만 이 3가지 문제는 해결할 수 없었습니다.
이 문제를 해결하기 위해 연구한 히포크라테스는 해결 방법 대신 히포크라테스의 초승달이라는 도형을 고안했습니다.
히포크라테스의 초승달은 고대 그리스 수학자 히포크라테스(Hippocrates of Chios, 기원전 5세기)가 연구한 기하학적 도형 중 하나로, 특정한 조건에서 원과 삼각형의 관계를 탐구한 결과입니다. 이 도형은 히포크라테스가 기하학적 문제를 해결하는 과정에서 제기한 흥미로운 사례입니다.
정의
히포크라테스의 초승달은 두 개의 반원으로 구성된 도형입니다. 이 반원들은 다음과 같은 방식으로 구성됩니다
- 직각삼각형이 주어집니다.
- 직각삼각형의 빗변을 지름으로 하는 반원을 그립니다.
- 직각삼각형의 각 변을 지름으로 하는 반원을 그립니다.
이 반원들 중 빗변을 지름으로 하는 반원에서 각 변을 지름으로 하는 두 반원을 제외한 부분이 히포크라테스의 초승달입니다.
성질
히포크라테스의 초승달은 기하학적으로 중요한 성질을 가집니다. 히포크라테스는 초승달의 면적을 구함으로써 원의 넓이를 삼각형의 넓이와 비교할 수 있는 방법을 제시했습니다.
히포크라테스의 초승달의 면적을 구하는 방법은 다음과 같습니다
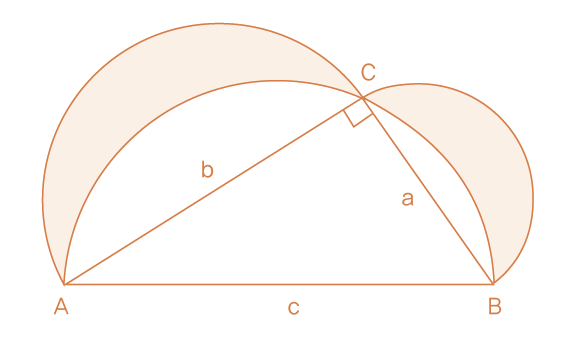

히포크라테스는 이 넓이들을 비교하여 초승달의 넓이를 구할 수 있었으며, 이를 통해 원의 넓이에 대한 이해를 발전시켰습니다. 그는 특히, 초승달의 넓이가 직각삼각형의 넓이와 같다는 점을 발견했습니다. 이는 원의 넓이와 삼각형의 넓이를 연관짓는 중요한 발견이었습니다.
역사적 의의
히포크라테스의 초승달은 고대 그리스 수학의 중요한 연구 성과 중 하나로, 원의 넓이를 구하는 문제와 관련된 초기 연구 중 하나입니다. 이는 후에 아르키메데스 등의 수학자들이 원주율(π)에 대한 연구를 진행하는 데 기초가 되었습니다.
히포크라테스의 초승달은 기하학적 탐구의 한 예로, 기하학적 문제를 해결하는 데 필요한 창의적 사고와 논리적 추론의 중요성을 보여줍니다. 이러한 기하학적 연구는 수학적 사고를 발전시키는 데 큰 기여를 했습니다.
오늘은 히포크라테스의 초승달에 대하여 알아보았습니다. 다음에 더욱 알찬 이야기로 오겠습니다.
감사합니다.
'수학이야기' 카테고리의 다른 글
| 질량과 무게 (0) | 2024.05.25 |
|---|---|
| 속력과 속도 (0) | 2024.05.07 |
| 방정식과 항등식(개념) 중1-1학기 (3) | 2024.05.01 |
| 연립방정식(개념)-중2-1학기 (0) | 2024.04.30 |
| 무한대 ∞ (4) | 2024.04.26 |




