한붓그리기(쾨니히스베르크의 7개다리)

오늘은 퇴니히스베르크의 7개 다리로 유명한 한붓 그리기에 대하여 알아보도록 하겠습니다. 

말 그대로 붓을 한 번도 떼지 않고 도형을 그리는 한붓그리기 그럼 시작해 볼까요?

 

 

한붓그리기란? 

붓을 한 번도 종이 위에서 떼지 않고 같은 곳을 두 번 지나지 않으면서 어떤 도형을  그리는 것을 말합니다.

한붓 그리기는 약 250년 전에 쾨니히스베르크(현재의 칼리닌그라드)에 있는 프레게르강에 걸쳐 있는 일곱 개의 다리를 모두 한 번씩만 건너갈 수 있느냐 하는 것으로 시작되었다고 합니다. 

 

 

쾨니히스베르크의 7개 다리

 

 

한붓그리기가 가능한 도형

 

쾨니히스베르크의 다리는 불가능하다는 것은 L. 오일러는 수학자가 증명하였습니다.

 L. 오일러는  '한 점으로부터 짝수 개의 선이 나와 있는 것을 우점(偶點), 홀수 개의 선이 나와 있는 것을 기점(奇點)이라 하면, 우점만으로 되어 있는 도형이나, 기점이 2개인 도형으로서 그 한쪽을 출발점, 나머지 하나를 종점으로 하는 경우에만 한붓그리기는 가능하다'는 한붓그리기의 '오일러의 정리'를 발표했습니다

 

L. 오일러는 이것을 연구하여, [그림]과 같은 선도(線圖)로 바꿔 7개의 선과 4개의 점으로 이루어진 것으로 하여 결국 조건대로 건너갈 수 없다는 것을 보여 주었다. 그 이유를 간단히 설명하면 다음과 같다. '한 점으로부터 짝수 개의 선이 나와 있는 것을 우점(偶點)-짝수점, 홀수 개의 선이 나와 있는 것을 기점(奇點)-홀수점이라 하면, 우점만으로 되어 있는 도형이나, 기점이 2개인 도형으로서 그 한쪽을 출발점, 나머지 하나를 종점으로 하는 경우에만 한붓그리기는 가능하다'는 것이다. 이것을 한붓그리기의 '오릴러의 정리'라고 한다.

조금 더 쉽게 정리하면,

1. 모든 점에서 짝수 개의 선이 만나는 경우, 즉 짝수점만 있는 경우에 한붓그리기가 가능합니다. 

2. 홀수점이 2개만 있으면 하나는 출발점, 다른 하나는 도착점이 되는 경우에는 한붓그리기가 가능합니다. 

 

홀수점(기점)이 0개 이거나 2개일 때 가능하다.

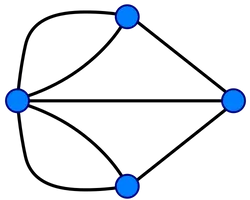
홀수점이 4개이므로 한붓그리기가 불가능하다

 

 

토막상식

레온하르트 오일러(Leonhard Euler)는 스위스의 수학자이자 물리학자입니다. 

수학, 물리학, 천문학 분야뿐만 아니라 의학, 식물학, 화학 등 다양한 분야에서 광범위한 연구를 진행한 사람입니다. 

수학 분야에서는 오일러의 등식, 수학기호 체계화 등의 업적을 남겼습니다.